假设我们有下面这样的一组二维的住房数据，我们的目标是利用住房面积和卧室的数量来推测房屋的价格：

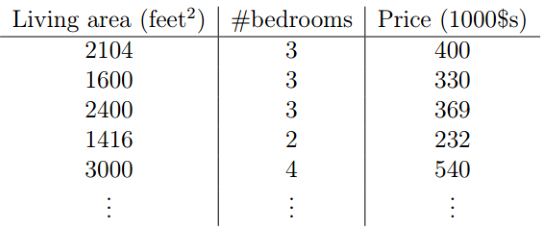
上述数据只有两个特征（面积和房屋数），我们可以给不同的特征赋予不同的权重 θ1, θ2，并加上一个偏移量 θ0 来构造一个线性模型来估计房屋的价格：

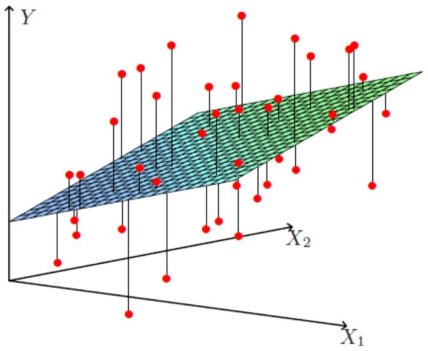
那么其表达式可以是这样的，其中θ都是未知的参数：

hθ(x)=θ0+θ1x1+θ2x2h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}

当然，我们还可以用向量的形式来表示，令：

θ=(θ0θ1θ2)\theta=\left(\begin{array}{l}{\theta_{0}} \\ {\theta_{1}} \\ {\theta_{2}}\end{array}\right)

x=(1x1x2)x=\left(\begin{array}{l}{1} \\ {x_{1}} \\ {x_{2}}\end{array}\right)

则有：

hθ(x)=∑i=0nθixi=θTxh_{\theta}(x)=\sum_{i=0}^{n} \theta_{i} x_{i}=\theta^{T} x

其中x是来自于样本的已知的值，θ是未知的值。上述式子可以用于有更多特征的情况，例如还可以加上房屋的地理位置，房屋的高度等特征。此线性模型对于其他的数据也是同样适用的。

既然是估计，那么肯定是存在误差的，对于第 i 个样本而言，其真实值与估计值的关系可以表示为：

y(i)=y^(i)+ε(i)=θTx(i)+ε(i)y^{(i)} = \hat {y}^{(i)}+\varepsilon^{(i)}=\theta^{T} x^{(i)}+\varepsilon^{(i)}

我们认为 ϵ 是一个误差值，所有样本的误差在真实值上下波动，所以 ϵ 是独立同分布的，可以理解为总体样本的误差服从均值为0，方差为 σ^2 的正态分布：

ϵ(i)∼N(0,σ2)\epsilon^{(i)}\sim N(0,\sigma^2)

令：

ε(i)=y(i)−y^(i)=y(i)−θTx(i)\varepsilon^{(i)}= y^{(i)} - \hat {y}^{(i)} = y^{(i)} - \theta^{T} x^{(i)}

则有：

y(i)−y^(i)∼N(0,σ2)y^{(i)}- \hat{y}^{(i)} \sim N(0, \sigma^{2})

于是得到了真实值 y 的分布：

y(i)∼N(y^(i),σ2)y^{(i)} \sim N(\hat{y}^{(i)}, \sigma^{2})

y 的概率密度函数为：

p(y(i)∣x(i);θ)=12πσexp⁡(−(y(i)−y^(i))22σ2)     =12πσexp⁡(−(y(i)−θTx(i))22σ2)p\left(y^{(i)} | x^{(i)} ; \theta\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}- \hat {y}^{(i)}\right)^{2}}{2 \sigma^{2}}\right) \\ \qquad \qquad \qquad \,\,\,\,\, = \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right)

由于样本的特征 x 以及它的真实值 y 均已知，上式可以看作是关于参数θ的函数，也就是似然函数。现在要做的就是求解参数θ的值，使得似然函数取值最大。令：

L(θ)=∏i=1mp(y(i)∣x(i);θ)     =∏i=1m12πσexp⁡(−(y(i)−θTx(i))22σ2)L(\theta)=\prod_{i=1}^{m} p\left(y^{(i)} | x^{(i)} ; \theta\right) \\\qquad \qquad \qquad \qquad \quad \,\,\,\,\, =\prod_{i=1}^{m} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right)

为了方便计算，对其取对数：

ℓ(θ)=log⁡L(θ)=log⁡∏i=1m12πσexp⁡(−(y(i)−θTx(i))22σ2)=∑i=1mlog⁡12πσexp⁡(−(y(i)−θTx(i))22σ2) =mlog⁡12πσ−1σ2⋅12∑i=1m(y(i)−θTx(i))2\ell(\theta)=\log L(\theta) \qquad \qquad \qquad \qquad \\\qquad \qquad \qquad \quad =\log \prod_{i=1}^{m} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right) \\\qquad \qquad \qquad \quad =\sum_{i=1}^{m} \log \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right) \\\qquad \qquad \qquad \qquad \, =m \log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{1}{\sigma^{2}} \cdot \frac{1}{2} \sum_{i=1}^{m}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}

因此，要让 L 最大，只需让下式最小即可：

J(θ)=12∑i=1m(hθ(x(i))−y(i))2J(\theta)=\frac{1}{2} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}

现在有了要优化的目标函数，可是θ的最优解是什么？要求解θ涉及矩阵的求导，可以参考机器学习中的矩阵基本求导公式。

∇θJ(θ)=∇θ(12(Xθ−y)T(Xθ−y))=∇θ(12(θTXT−yT)(Xθ−y))=∇θ(12(θTXTXθ−θTXTy−yTXθ+yTy))=12(2XTXθ−XTy−(yTX)T)=XTXθ−XTy\nabla_{\theta} J(\theta)=\nabla_{\theta}\left(\frac{1}{2}(X \theta-y)^{T}(X \theta-y)\right) \qquad \qquad \\ \quad =\nabla_{\theta}\left(\frac{1}{2}\left(\theta^{T} X^{T}-y^{T}\right)(X \theta-y)\right) \\ \qquad \qquad \qquad \quad =\nabla_{\theta}\left(\frac{1}{2}\left(\theta^{T} X^{T} X \theta-\theta^{T} X^{T} y-y^{T} X \theta+y^{T} y\right)\right) \\ \quad =\frac{1}{2}\left(2 X^{T} X \theta-X^{T} y-\left(y^{T} X\right)^{T}\right) \\ =X^{T} X \theta-X^{T} y \qquad \qquad \qquad

令上式子等于 0 求得驻点：

θ=(XTX)−1XTy\theta=\left(X^{T} X\right)^{-1} X^{T} y

此时 θ 即为最优解。